Autonomous Vehicle Robotic Wheel Drive
| Robotic Wheel Drive | |
|---|---|
| Client/Sponsor: | Bastian Solutions |
| Team Name: | Basti-Boys |
| Duration: | Fall 2017 - Spring 2018 |
| Faculty Adviser: | Dr. Matthew Swenson |
| Mentor: | Coleton Bailey |
| Team Members: |
|
The purpose of this project is to create a compact high torque/rpm robotic wheel drive for Bastian Solution's autonomous warehouse robot.
Problem Definition[edit | edit source]
Background[edit | edit source]
Bastian Solutions has a current WDS (wheel drive system) that uses 30% of the vehicles length and 50% of the vehicles width. The axial length of their current design is approximately 8.8 inches, with the motor contributing to most of the assembly's axial length. It is desired to decrease the WDS assembly to at least 4.4 inches so that other features can be added to the vehicle. For their current motor to meet the required torque/rpm and power conditions, it uses a 4:1 planetary gearbox. A planetary gearbox was chosen because it has advantages over other gearboxes that work well in this application.
Pertinent planetary gearbox advantages:
- Naturally compact, but can supply high reduction ratios (reduces WDS axial length, most motors cannot supply the required torque without modification)
- Inline or coaxial design allows input shaft to be inline with gearbox (saves radial space)
- Generally have low backlash (vehicle must move with precision)
- The nature of their design distributes internal gearbox loads more equally (WDS undergoes high loadings)
- Long life and efficiency (gearboxes are expensive to replace and they add to mechanical energy loss)
For them to add more features and to further optimize the vehicle design, they must decrease the volume of the WDS. They require the WDS to be capable of meeting two primary torque/rpm conditions as well as moving a payload up to 100 lbs.
Specifications[edit | edit source]
| Variable | Condition A: 100lb payload | Condition B: 50lb payload | Condition C: 100lb payload |
| Torque | 2340 oz-in | 1970 oz-in | 500 oz-in |
| Speed | 275rpm (3ft/s) | 366rpm (4ft/s) | 750rpm (8ft/s) |
| Acceleration | 4ft/s^2 | 4ft/s^2 | 8ft/s^2 |
| Duration of Load | 10 seconds | 7.5 seconds | The vehicle will spend most of its time in this condition |
Volumetric Constraints
The full WDS assembly must not exceed 4.4 inches in axial length nor 8 inches diametric length.
Iterative Design[edit | edit source]
Sub-Systems[edit | edit source]
Our first step was to break the WDS into 3 sub-systems:
- Motor
- Gearbox
- Output Shaft
Concepts Considered[edit | edit source]
| Concept | Pros | Cons |
| 3:1 Planetary Framo-Morat Gearbox & Stacked Framless Kollmorgen Motors | 3.5 inch assembly length,
High Torque |
Low speed motors (require high voltage),
Two motors means twice the current required, Framo-Morat Gearboxes have high lead times and are expensive |
| 6:1 Planetary Framo-Morat Gearbox & TG5153 Thin Gap Motor | 3.3 inch assembly length,
Motor meets OSHA standards and torque/Rpm needs |
Framo-Morat Gearboxes have high lead times and are expensive |
Design Procedure For Prototype 1[edit | edit source]
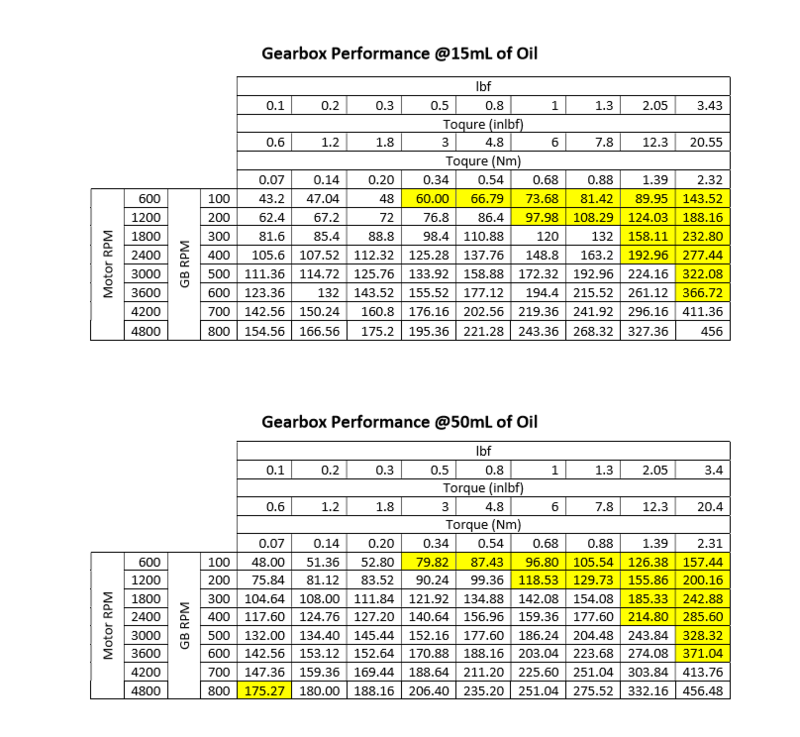
The biggest constraint is the volumetric constraint of about 8 inches in diameter by 4.4 inches axially. The strategy is to find the thinnest motor who's diameter is at least half an inch smaller than the 8 inch diametric constraint. The motor has to be thin enough to leave room for the gearbox and bracket, while also being capable of providing a reasonable torque/rpm.To figure out what would be a "reasonable" torque/rpm from the motor, one of our members performed an analysis. The analysis showed the different torque/rpms the motor would need to provide using different gear reduction ratios to meet the torque/rpm requirements. Using this method allowed for the gearbox ratio selection process to be easier. The ring gear's outer diameter was constrained to 6 inches to allow for ~2 inches of ground clearance. The torque/rpm vs. gear ratio table and the maximum diameter of the ring gear were used to maximize the pitch diameter of the sun gear to increase its load bearing capabilities.
Motor Selection[edit | edit source]
Dimensional Analysis[edit | edit source]
Our torque and spatial requirements for our motor led us to investigate pancake-servo motors. Three brushless series pancake-servo motors from three different companies stood out: Printed Motor Work's motors, Koll-Morgen’s motors, and the Thin Gap's motors. Pancake-servo motors have a very high torque constant and a relatively low motor constant which allow for high torque at low voltages. This combination was essential for our needs. We found that a space constraint of less than 7.2” in diameter (referenced to our axle) would be critical to meet our space constraints, as well as an axial length of less than 3.4 inches for the motor and gearbox combination.
Power Analysis[edit | edit source]
To meet the power constraints, the team created a table in Excel that approximates electrical power required for a given torque, speed, and gearbox ratio. The inputs of the table were the motor constants, mechanical and electrical restrictions of the motor, and the power restrictions from the client. The table used the below governing equations:
The selection process involved recording a motor’s specifications into the table and then iteratively changing the gearbox ratio until the motor met every requirement. If the motor didn’t meet all of the requirements within a gearbox ratio range of 2:1-6:1, then a new motor was selected and the process repeated. Eventually, after many iterations, two motors became prime candidates; the TG5152 and the TG5153.
Thermal Analysis[edit | edit source]
The next step was to perform a parametric study on the heat dissipation (W) of the motor in relationship to power supply and various torque and speed combinations. An electric motor will dissipate heat due to resistance in the coils and damping from lubrication. Considering the gearbox and bearings, the damping coefficient, B, was estimated to be 0.001- 0.003 (Nm∙s)/rad. A Matlab script (below) was written to produce the heat dissipation due to power-loss.
The input values for the script were k_t, k_e, R, and B. To calculate the power-loss, the equations for Voltage and Current were used above along with the below electrical and mechanical power equations.
Gearbox Design[edit | edit source]
Gear Design and Selection[edit | edit source]
Casing design[edit | edit source]
Spatial Analysis
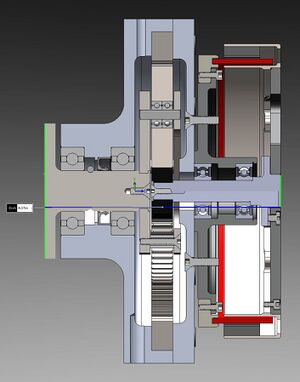
For our gearbox design to meet our spatial requirements we need to design our casing to be as slim as possible. We are hoping to incorporate our mounting bracket into our gearbox design so that we can eliminate the need for more bearings and space usage in our final assembly.
Thermal Analysis
The high torque and RPM operating range of our gearbox means that we will need to consider the thermal characteristics of our gear operation. Most planetary gear trains produced today are over 95% efficient, however that does mean that a certain portion of mechanical energy is translated into heat caused by frictional losses. Due to the prototype nature of our design we will simply estimate our inefficiency in order to determine how much energy must be dissipated away from our gearbox. If not managed, the heat generated by the gearbox can lead to damage to our gear teeth and ball bearings, severely reducing the life span of our gearbox. We are looking into using aluminum for the gearbox casing as this gives us much higher thermal conductivity and helps cool our gears and bearings.
Manufacturability Analysis
In order to deliver a cost-effective design we must simplify our part geometry and create a design that can be produced quickly and efficiently. To accomplish this we are focusing on a design that minimizes CNC tool changes and allows for use of larger cutting tools to reduce time spent fabricating. Using aluminum will also speed production as it is a soft metal and will process quickly on a mill for production.
Carrier Plate Design[edit | edit source]
Fatigue Analysis
Our design must be durable and not allow the carrier plate to crack after years of abuse. To accomplish this we will design for infinite lifespan with a loading safety factor. The primary concerns in designing for this is how we mitigate stress concentrations at the planet gear pins and our output shaft. We also want to minimize weight and rotational inertia so we can maximize our gearbox efficiency.
Material Analysis
Due to the reversed nature of our loading we need a fairly ductile material that won’t crack due to repeated loadings in multiple direction.
Manufacturability Analysis
Low cost and speed of production are critical for this piece, ideally we can create this from a flat cut profile to reduce fabrication costs.
Shaft Design Analysis[edit | edit source]
Bearing Analysis[edit | edit source]
Prototype 1[edit | edit source]
Prototype 1 features a TG5153 Thin Gap motor and a single stage custom 6:1 planetary gearbox. Its dimensions are 4.5L x 6.1W x 6.1H inches. The neck of the gearbox is designed to accommodate two ball bears to absorb a radial load of 117 lbs. The TG5153 is a high torque density brushless DC motor capable of producing 3.5Nm of torque, and 20Nm with the gearbox. The dry weight of the gearbox is 8.6 lbs which is 30% lighter than Bastian Solutions current gearbox.
Validation[edit | edit source]
For testing procedures and results refer to the Archives.
Archives[edit | edit source]
SW Drawings[edit | edit source]
Presentations[edit | edit source]
Budget[edit | edit source]
Schedule[edit | edit source]
Meeting Minutes[edit | edit source]
Validation[edit | edit source]
Team Members[edit | edit source]
| Team "The Basti-Boys" | ||
|---|---|---|
| Member | Biography | Discipline |
| Brad Morris | Brad is a senior in Mechanical Engineering looking to graduate in May 2018 from the University of Idaho. In his free time he enjoys target shooting and dirt bike riding, both of which are among reasons why he chose to pursue engineering. His favorite aspect of the robotic wheel project thus far has been the project learning associated with group and personal efforts. | Mechanical Engineering |
| Daniel Hein | Daniel Hein is a senior studying Mechanical Engineering. He is looking to graduate in May 2018. He enjoys hiking, car repairs, and mountain biking, which encourage him to study mechanical engineering. His favorite aspect of this project has been learning more about FEA tools and material selection for gearbox design. | Mechanical Engineering |
| Gabriel Riggs | Gabe grew up most of his life in Pocatello, Idaho where he attended Century High School. His favorite sports are track, wrestling, and Judo. His hobbies are playing the guitar and programming for fun. After graduating from the University of Idaho he plans on going to graduate school to get his Master’s degree in Mechanical Engineering and maybe a Minor in Electrical Engineering just for kicks. | Mechanical Engineering |
| Jacob Riggs | Jacob is a senior, and is hoping to graduate in the Fall of 2018. He enjoys drinking freshly brewed, Aged Earl Grey tea on a cool rainy day while working on his book, as well as hiking and camping, taking stuff apart too see how it works, and designing mechanical things. His favorite color lies between 470nm and 480nm of the color spectrum. His favorite part about this project is that it has every aspect that he wants to do as a ME. | Mechanical Engineering |